The n-cube playground

As a playground to understand the curse of dimensionality we spread 20,000 points throughout a 10-dimensional cube of side 2. Each coordinate of a point is independently chosen from a uniform random distribution ranging from -1 to 1. While the points are uniform in the ten dimensional cube, that will not be the case if we project them along a line that crosses the center of the cube

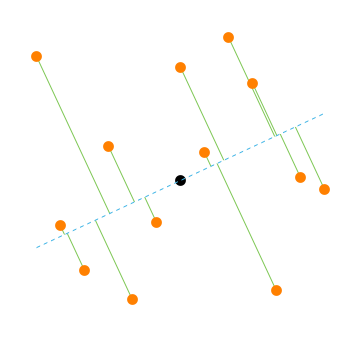
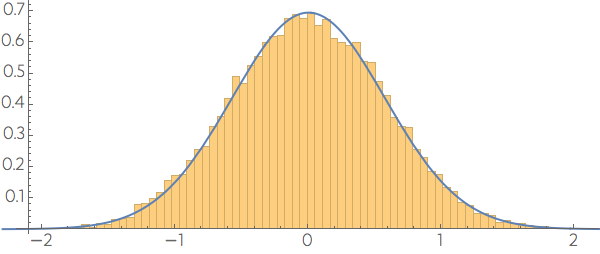
The points appear to be concentrated near the middle of the line. If the line is in a random direction, the density distribution of the points will look Normal along the line

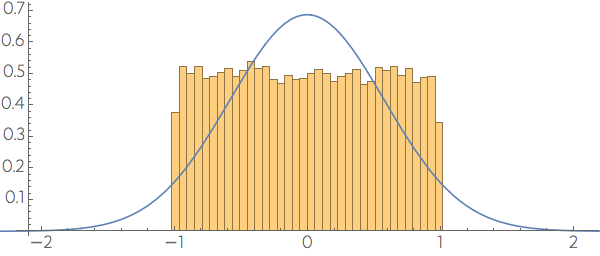
but if we choose one of the coordinate directions we still get a distribution symmetric around the center, but uniform

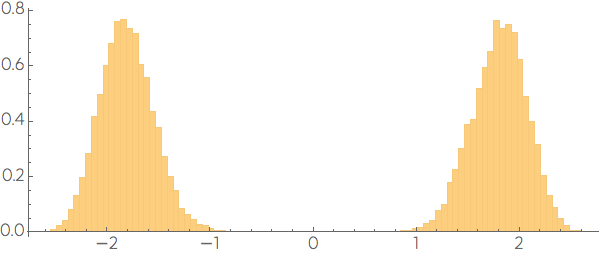
and if we choose the big diagonal of the cube, the distribution of points will look the closest to Normal among all possible directions

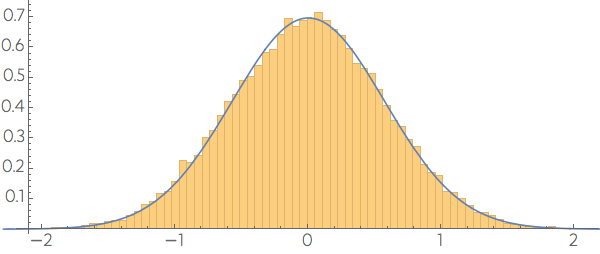
To understand why we see a non uniform distribution for a random direction, consider the projection process. At some point it requires the dot product between the vector $\mathbf{x}$ with the tip on the point and the random direction $\mathbf{w},$ which is a sum $\sum w_i x_i.$ From the central limit theorem we know that this sum will be Normal distributed.

First surprise

The projections of the uniformly distributed follow a Normal distribution with mean zero, which may give the impression that there are many points near the center of the cube. But if we plot the distance of these points from the origin we discover that there are very few points near it. (To show that the data is symmetric on a coordinate, we sort all points based on the sign of the first coordinate, plotting as $-d$ a point a distance $d$ with $x_1<0.$)